Introducing pufferfish An efficient index for the colored, compacted, de Bruijn graph

Note: This post describes some cool data structure work (link to the work-in-progress GitHub repo here) my students @fataltes, @hrksrkr, and I have been doing (pre-print coming soon!).  If you find these ideas interesting, or you have any interesting thoughts or suggestions, I’m sure they’d appreciate a shout out!

Though the de Bruijn Graph (dBG) has enjoyed tremendous popularity as an assembly and sequence comparison data structure, it has only relatively recently begun to see use as an index of the reference sequences (e.g. deBGA, kallisto). Particularly, these tools index the compacted dBG (cdBG), in which all non-branching paths are collapsed into individual nodes and labeled with the string they spell out. This data structure is particularly well-suited for representing repetitive reference sequences, since a single contig in the cdBG represents all occurrences of the repeated sequence. The original positions in the reference can be recovered with the help of an auxiliary “contig table” that maps each contig to the reference sequence, position, and orientation where it appears as a substring. The deBGA paper has a nice description how this kind of index looks (they call it a unipath index, because the contigs we index are unitigs in the cdBG), and how all the pieces fit together to be able to resolve the queries we care about.  Moreover, the cdBG can be built on multiple reference sequences (transcripts, chromosomes, genomes), where each reference is given a distinct color (or colour, if you’re of the British persuasion). The resulting structure, which also encodes the relationships between the cdBGs of the underlying reference sequences, is called the “compacted, colored de Bruijn graph” (ccdBG).  This is not, of course, the only variant of the dBG that has proven useful from an indexing perspective. The (pruned) dBG has also proven useful as a graph upon which to build a path index of arbitrary variation / sequence graphs, which has enabled very interesting and clever indexing schemes like that adopted in GCSA2 (which we won’t discuss further here, but which I hope to cover in more detail in a future post).  Also, thinking about sequence search in terms of the dBG has led to interesting representations for variation-aware sequence search backed by indexes like the vBWT (implemented in the excellent gramtools package).

Here, however, we focus on indices built directly on the ccdBG, and we further focus on schemes based on indexing this structure by hashing the k-mers it contains.  While there are many benefits to other indexing data structures (e.g. full-text indexing structures like those built on the suffix tree, (enhanced) suffix array, FM-index etc.), there are certain very nice properties of hashing-based schemes.  Often, they are simple to understand and think about, and they can generally be made to have small constant factors, making them very fast for lookup (which is one of the primary reasons we’re interested in pursuing such a scheme).

While existing hash-based indices based on the cdBG (and ccdBG) are very efficient for search, they typically occupy a large amount of space in memory (both during construction and once built). As a result, to make use of such data structures on large reference sequences (e.g., the human genome) or collections of reference sequences (e.g., in a metagenomic or microbiomic context), one typically requires a very large memory machine — if the structures can be built at all.

Recently, we’ve been working on a pretty nifty new data structure (at least my students and I think it’s nifty, anyway).  This new and more compact data structure is implemented in our new software,  pufferfish, for indexing the ccdBG. While maintaining very efficient queries, this allows pufferfish to index reference sequences while reducing the memory requirements considerably (by about an order-of-magnitude compared with existing hash-based solutions when we adopt the sparse variant of our index). This greatly reduces the memory burden for indexing reference sequences and makes it possible to build hash-based indexes of sequences of size that were not previously feasible.

Pufferfish supports (i.e., implements) two types of indices — called dense and sparse indices. Both of these make use of an efficient minimum perfect hash implementation to vastly reduce the memory requirements compared to other hashing-based dBG, colored-dBG, and compacted-colored-dBG indices. However, the sparse index saves even more space by only directly storing the position for certain k-mers (and inferring the positions dynamically for the rest).

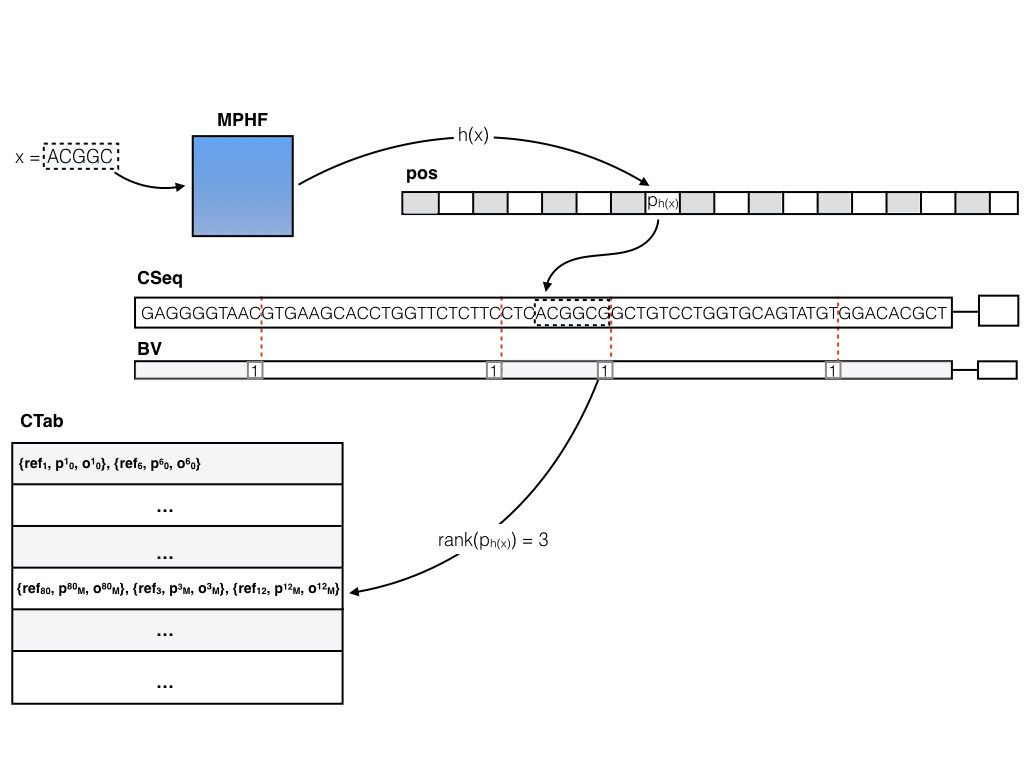
The basic (dense) pufferfish index

The basic (dense) pufferfish index can be visualized as in the image below:

The contigs of the compacted dBG are stored contiguously in a (2-bit encoded) vector CSeq, and a boundary bit vector BV marks the end of each contig. All of the N valid k-mers (i.e. k-mers not crossing contig boundaries) are indexed in a minimum perfect hash function. A k-mer query (i.e., does this k-mer exist in the index, and if so, where does it occur in the reference?) is answered by consulting the MPHF h().  Compared to traditional hashing approaches, this can save a tremendous amount of space, since the hash function spends about 3 bits per key (k-mer), regardless of k (whereas traditional hashes might spend 8-12 bytes, or more, as they have to store the key explicitly and maintain a reasonable load factor). For a k-mer x, if 0 <= h(x) < N, either x != CSeq[pos[h(x)] : pos[h(x)] + k], in which case x does not appear in the ccDBG, or pos[h(x)] stores the position of x in CSeq. Efficient rank and select queries on the BV vector (we’re currently using the excellent SDSL-lite library for such things) can be used to determine the relative offset of x in the contig (say c) where it occurs, and to lookup all occurrences of c in the reference sequence. This information is encoded in the contig reference table (CTab), which records the reference sequence, offset and relative orientation of all occurrences of c in the reference.  Pufferfish also records and stores in the index (though this is not actually required to answer the basic k-mer queries) the equivalence class of each contig in terms of the reference sequences where it appears (i.e. two contigs belong to the same equivalence class if they belong to exactly the same set of transcripts / genomes / etc.).  This information can be useful for fast mapping algorithms.

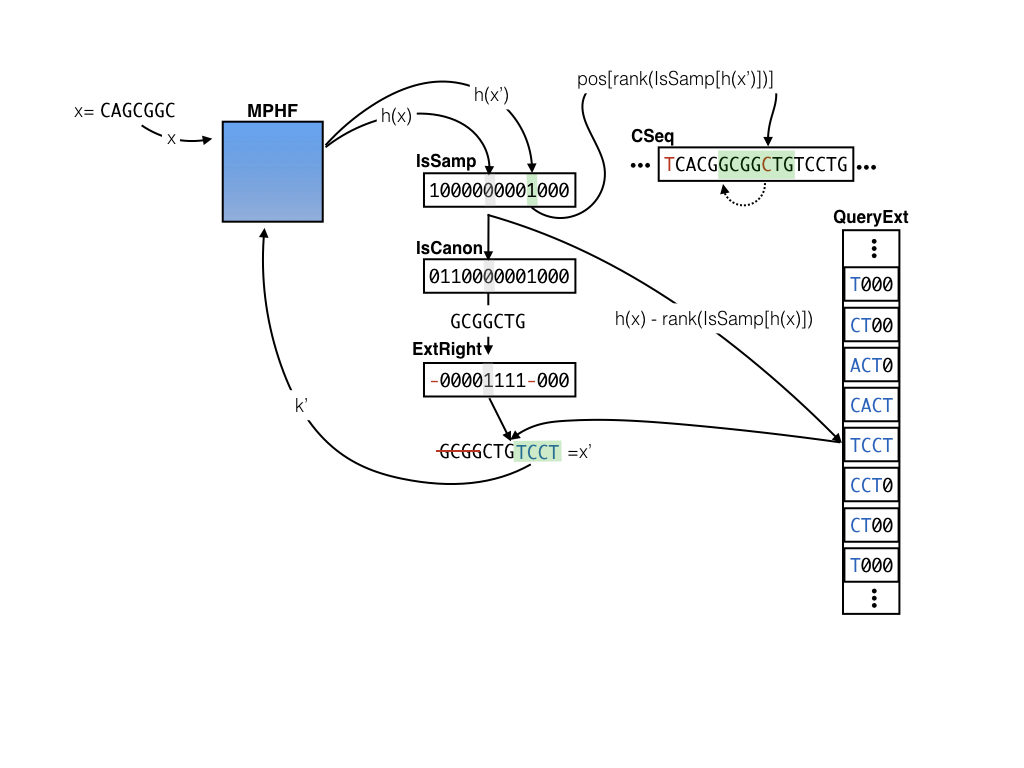
The sparse pufferfish index

In addition to the tables maintained in the dense index, the sparse index also records 4 other pieces of information. There are 3 extra bit-vectors (IsSamp, IsCanon, and ExtRight) and one extra packed integer vector (QueryExt). The sparse index builds on the observation that any valid k-mer in the cDBG is a distinct k-mer that is one of :

1. a complex k-mer (it has an in or out degree > 1)
2. a terminal k-mer (it starts or ends some input reference sequence)
3. a k-mer with precisely one successor / predecessor

Instead of storing the position for every k-mer (which requires bits per entry), the sparse index stores positions for only a sampled set of k-mers (those where IsSamp is 1) — so that pos becomes considerably smaller. For k-mers whose positions are not stored, the QueryExt table records which nucleotides should be added to either the beginning (if ExtRight is 0) or end (if ExtRight is 1) of the query k-mer to move toward the nearest sampled position. We also need to know if the variant of the k-mer that appears in the CSeq table is canonical or not (hence the IsCanon vector). In this scheme, successive queries and extensions move toward the nearest sampled k-mer until a position can be recovered, at which point the implied position of the query k-mer can be recovered and the rest of the query process proceeds as in the dense index. By trading off the rate of sampling and the size of the extension that is stored (e.g., 1, 2, 3, … nucleotides), one can trade-off between index size and query speed. A sparse sampling and shorter extension require more queries to locate a k-mer, but result in a smaller index, while a denser sampling and/or longer extensions require fewer queries in the worst case, but more space. If the extension size (e) is , where s is the sampling rate, one can guarantee that at most one extra query need be performed when searching for a k-mer. The sparse index is currently in the develop branch of pufferfish, and should make it into master soon.

Here is a visual example of querying for the position of k-mer x=CAGCGGC in CSeq where s = 9 and e = 4. We find that the entry corresponding to x is not sampled, and that IsCanon is false and the corresponding bit for IsCanon says that the k-mer stored in CSeq is not canonical. Since x is canonical, we take the reverse complement to get GCGGCTG. We then consult the ExtRight vector to determine the extension TGTC should be applied to the right of the k-mer GCGGCTG. After applying this extension we get our new key x’ = CTGTCCT, which we then look up again in the MPHF. This time, we see that IsSampled[h(x')] = 1, so we can retrieve the index for x' at p_{x’} = pos[rank(IsSampled[h(x')])] (since we only store the positions for the sampled k-mers). Finally, since we know that we extended the canonical k-mer to the right by 4 bases to obtain x', we look for our original query at pos[rank(IsSampled[h(x')])] - 4, leading us to find (in this case) the reverse complement of our original query key GCGGCTG.

One key here is that if we keep only sampled positions in the pos vector, and the extension entries for only the non-sampled positions in the QueryExt vector, then, for a key x that hashes to an index h(x) = i we can retrieve the position in pos[rank(IsSamp[i])] if IsSamp[i] is 1 and we can retrieve the extension nucleotides at QueryExt[i-rank(IsSamp[i])]otherwise.  This makes access to all of the auxiliary information to perform the sample “jumping” efficient — all we need are lookups on the bitvectors and rank on the IsSamp vector in particular.  So, why does this index save us space?

In the sampled index we require 1 extra bit per valid k-mer (IsSamp).  For each of the non-sampled k-mers we require 2*e (forQueryExt) + 3 (one for each of the new bit vectors) + lg(e) (to remember the extension size) bits.  When one chooses e and s intelligently, this can be considerably less than the storage requirements of the dense index.  Now, note that there is an even more compacted scheme for storing the actual extension characters (the other bit vectors are still required) — one that uses 2*e' +lg(e) bits to store each extension of size e' <= e.    Here, e' is the actual length of the extension, not the maximum extension length, and in expectation this is equal to e. This requires a fast data structure for static prefix-sum, which we haven’t yet implemented (if you know of one with a nice C++ implementation, please let us know!).

Under this sampling scheme, we only store positions for (roughly) 1 out of every s k-mers.  WhenCSeq is large, and these positions require 4,5,…8 bytes each, these savings are considerable.  If one is willing to perform more iterations of the query procedure described above for non-sampled positions, she can make the extension size shorter and the sampling factor larger.  That is, this process can be applied iteratively and one can find the next sampled position in at most extension jumps in the worst case.  This slows down queries by a constant factor, but reduces the size of the index by a similar factor.  We note that, in the extreme case, one could dispense with the extension vector entirely, and simply try each of the 4 possibilities (i.e., ) for the predecessor / successor of a query; however, we require an extension size of at least 1 for reasons of performance in the pufferfish implementation.

A sneak-peek at pufferfish

Pufferfish is still very much a work in progress.  We’re still in the process of tweaking aspects of the representation to optimize time / memory, and we are benchmarking different data structures for the pufferfish preprint, the first version of which should land soon.  However, the initial results are very promising.  For example, we can take a look at how pufferfish compares in terms of index size and lookup time to the other hashing-based ccdBG indices (those implemented in deBGA and kallisto) for data of two different sizes; the human transcriptome and the human genome.  The former of these is a relatively small reference sequence, but with considerable shared sequence complexity induces (mainly) by alternative splicing.  The latter of these is a reasonably large reference sequence with a tremendous amount of repetition, including some very complex and some simple regions of the compacted dBG.  First, we look at the sizes of the dense and sparse pufferfish indices, as well as that of kallisto and deBGA for the human transcriptome:

Table 1 (transcriptome indexing)

So, we see that even on a relatively small reference (the transcriptome reference — gencode v25 protein coding transcripts — is 201MB), and even when using the dense pufferfish index, we obtain considerable savings over the other methods, with the dense pufferfish index being about 6.7x smaller in memory than the closest alternative representation.  Of course, while these numbers represent considerable overhead for the index (relative to the size of the text itself), the transcriptome is small enough that this doesn’t pose too much of a problem.  However, when the size of the reference we wish to index becomes larger, so do our resource requirements … and by a considerable margin.

Table 2 (genome indexing)

Again, we see a similar trend, except that this time the expansion in the index size considerably increases the memory burden.  These indices can get big fast.  This means that, using existing hashing-based cdBG indices, you may need a reasonably large-memory server to index references like the human genome, and you might not even be able to index much larger references (e.g., much larger genomes or large collections of microbial genomes).

Also, you might notice the ‘*’ next to the deBGA numbers here.  This is because these numbers are approximate and taken from the deBGA github repository.  It’s worth noting that these numbers are for k=22, and so one might expect the proper index to be even larger when using the same parameters we used here for the other tools (k=27).  The reason for this using these numbers is that we ran into an issue when using deBGA to index the human genome.  It produced an index that was, in fact, around the same size as the (dense) pufferfish index.  This was smaller than we’d expected, and a further inspection led us to discover that, despite the fact that index construction completed (i.e., the program ran and reported successful termination), it seemed to be storing information for only 1,332,190,304 distinct k-mers.  However, pufferfish and kallisto both agree that there are 2,579,117,522 distinct k-mers in this particular version of the genome (GRCh38 primary assembly).  So, for some reason, deBGA seems to only be indexing about half of the k-mers here (there could, of course, be user error).  If we “extrapolate” the numbers, however, we can see that doubling the index size (to account for a 2 fold increase in the number of indexed k-mers) would make the index size and memory usage approximately agree with what is reported in the deBGA github repo.  We intend to keep digging to figure out what’s going on here, and have filed the relevant reports at the deBGA GitHub repo, but the numbers in Table 2 above seem to agree fairly well with what is reported in the deBGA repository and what we might expect extrapolating the results we obtained.  Regardless, we can’t do lookup (i.e., speed) tests with deBGA until we find out why it seems to not be locating all of the indexed k-mers.

Lookup Speeds

The other result of interest here is lookup speed — that is, given a query k-mer, how fast the index can recall the reference loci where the k-mer appears (or report if the k-mer doesn’t, in fact, appear in any reference).  You may not always want to recall all the reference positions, and may, instead, wish to recall some associated information for the k-mer (like the equivalence class etc.).  In theory, all three indices discussed above support these queries, though deBGA does not currently compute or store equivalence class information.

Currently, pufferfish is only an indexing data structure and not a full mapper or aligner.  So, to try and make a fair comparison, we benchmarked some query operations for k-mer lookup. Specifically, we retrieved the total number of hits — i.e. total number of reference loci matches — for all of the k-mers in a set of reads.  Currently, we have not figured out how to include deBGA in this benchmark, due mainly to the issue described above (i.e., it seems not to be indexing all of the k-mers and hence doesn’t give a result that agrees with the other tools, precluding a meaningful speed comparison).

Nonetheless, we can compare k-mer lookup speeds to those of kallisto (which are blazingly fast, since it is essentially lookup in an un-compressed hash table of k-mers to the relevant contig information).  We find that the dense pufferfish index has k-mer query performance that is only a little bit (25-30%) slower than that of kallisto.  The extra timing overhead mostly comes from the fact that the minimum perfect hash lookup tends to be a bit slower than what one gets in a normal hash, and that to obtain the contig-relative position of a k-mer from the global position requires a select operation on BV (it also requires rank, but that tends to be very fast).  Lookup in the sparse pufferfish index (with an extension size of 4 and a sampling factor of 9) tends to be about 3-3.5X slower than the dense index.  This is still quite fast, as the average query time per k-mer (for an index over the genome) in the dense index is ~133 ns while for the sparse index this is ~ 468 ns ^[1]running in a single thread on an Intel(R) Xeon(R) CPU E5-2699 v4 @ 2.20GHz.  This difference somewhat tracks the size difference regarding the size of positional information being stored (e.g., for the human genome, the dense index uses ~2X more space to store k-mer position information compared to the sparse index — 9.7G vs 4.8G — though the total difference in index size is a smaller factor because other structures remain the same).  However, it’s also the case that there is considerable room for optimization in the sparse query code, so it’s very likely the gap can be closed further.

Given the reduction in space achieved by both the dense and sparse pufferfish indices, we find these initial results very promising.  The dense index can provide a much more compact index than a traditional hash-based approach, with very little sacrifice in speed.  On the other hand, the sparse index can provide an order of magnitude reduction in (in-memory) index size, while still providing very efficient queries, albeit slower than the dense index or traditional hash tables.  Again, it’s worth noting that the sampling scheme adopted by the sparse pufferfish index provides a “knob”.  These numbers represent the “fast” end of the knob (one need perform at most one extra extension and lookup operation for a given k-mer query), but more extreme sampling values have the potential to reduce the space required for storing positional information much further.

One final interesting point worth noting is that, due to it’s smaller size and layout on disk and in memory, the pufferfish index can be faster to load than traditional hash-table-based indices when the reference is large.  This is partly because “de-serializing” a hash-table basically amounts to re-inserting all of the elements, and partly because some of our auxiliary information is stored in a format more appropriate for reading large chunks of memory at once.  This can lead to some interesting scenarios where pufferfish (dense) is actually faster to load the reference and query many k-mers than other indices that otherwise have a slightly faster per-query time.  For example, to load the genome index and query all of the k-mers from a set of 33.4M, 100bp reads (using a single thread), took pufferfish 6m 56s and took kallisto 11m 55s.  Of course, for any type of index that will be used to make queries over many different sets of reads, it would make sense to engineer a shared-memory index so that one need pay the index loading cost only once and can keep the index in memory that can be mapped by multiple processes until all of the querying is complete.  It’s also true, of course, that the engineering effort that needs to go into a cross-platform and robust shared-memory implementation is non-trivial ;P.

Some practical considerations and upcoming improvements

So, the pufferfish index already looks like it’s doing a pretty good job at providing an efficient ccdBG index in terms of both memory usage and query performance.  However, there are still quite a few places for improvement.  For example, right now, the contig table stores the list of reference sequences, offsets and orientations for each contig using a vector of vectors where the reference sequence id and offset are stored with fixed-width integers.  This potentially wastes considerable space when the number of reference sequences is < 4,000,000,000 and when the longest reference sequence (i.e., transcript or chromosome) is < 4,000,000,000.  By replacing this array of structures layout (AoS) with a structure of arrays (SoA), we can pack the reference id and reference offsets into the appropriate number of bits, thereby reducing the space of the contig table.  Further, there is still considerable room for improving the performance of querying in the sparse index.  We’ll be working on this in the immediate future, and then likely turning the pufferfish index into a fully-fledged mapper / aligner.  We are also very interested in exploring how this data structure, and algorithms we can build on top of it, will be useful when indexing a large collection of different sequences — there seem to be many potentially interesting applications in metagenomics and microbiomics.

Another practical consideration worth mentioning is the following.  Pufferfish is a method to index and query the ccdBG, not to construct it outright.  Pufferfish expects as input a GFA format (currently GFA v1) file containing the ccdBG — this has a segment for every contig, and a path for every reference sequence, and subsequent contigs in a reference path must overlap by exactly k-1.  We rely on other excellent software to generate these GFA files for us.  Currently, we’re using TwoPaCo to generate the ccdBG.  TwoPaCo adopts an interesting multi-stage and highly-parallel algorithm that constructs the compacted dBG directly (without fist constructing the un-compacted dBG).  It works very well, and can compute the cdBG for even relatively large reference sequences quickly and in limited memory.  Unfortunately, all is not perfect with this pipeline, as TwoPaCo makes a few assumptions (e.g. like this, and this) that prevent us from using its GFA directly.  So, we have build a “pufferize” tool that takes the TwoPaCo format GFA and converts it into a GFA that is of the appropriate format to be indexed by pufferfish (there’s actually some interesting considerations here when transforming the “near cdBG” into the cdBG we expect, but that’s fodder for another post).  While this has worked well for all of our testing, it, unfortunately, adds time, resources, and a bit of clunkiness to the whole procedure.  So, we’re also looking for more efficient ways to directly get the input we need — a compacted dBG, in GFA format, where each segment is of length at least k and all segments in a path overlap by exactly k-1 nucleotides, and there are no repeated (canonical) k-mers.  If you know of any software that efficiently outputs this, please let us know!  Finally, we welcome any thoughts or feedback on pufferfish (e.g., ideas for improvements and cool features), and keep a lookout for the pufferfish pre-print, which should be coming very soon!

Edited (07/03/2017) to add some clarifications and fix a few typos.

Edited (07/03/2017, 9:25PM) to update some numbers (puffer got better!).

Edited (07/04/2017, 12:02PM) to update some numbers (puffer got better on the transcriptome!).